What is Stokes' Law?


Stokes’ Law is the key to modern centrifugation. Understanding it—and its implications—has had a huge impact on an unlikely array of businesses: dairies, breweries, manufacturing facilities and machine shops, ethanol plants, and more.
But why Stokes’ Law is so important isn’t immediately obvious.
Textbook definitions will tell you that Stokes’ Law states the following:
“The force required to move a sphere through a given viscous fluid at a low uniform velocity is directly proportional to the velocity and radius of the sphere.”
As a formula, it’s usually written like so:

Written this way, Stokes’ Law is a handy way to calculate the force of viscosity (aka “drag force”) a viscous fluid exerts on objects falling through it. But that’s only true when:
- the falling objects are essentially spherical, have a low tendency to create turbulence in the fluid, and do not meaningfully interfere with each other
- the fluid itself is uniform and has a “laminar” (that is, smoothly layered) flow
- and the objects and fluid all interact primarily with smooth surfaces
Given all that, Stokes’ Law seems like a niche formula, more useful for calculating the terminal velocity of an 8 ball dropped into a vat of honey than figuring out how to better extract distiller’s corn oil (DCO) from ethanol or get the tramp oil out of your sumps.
Applying Stokes’ Law
Let’s start by considering what a mixture of oil and water really is: droplets of one fluid trapped in another. True to the conditions of Stokes’ Law, those droplets are smooth spheres (albeit microscopic ones). They won’t tend to create turbulence when moving (physicists would say they “have a low Reynolds number”). They’re trapped in a fluid that is perfectly happy exhibiting neatly layered flow—provided it’s flowing in a smooth-walled environment (like Italian dressing sitting in a glass bottle on the table or cutting fluid resting in a settling tank).
As a result, Stokes’ Law does indeed correctly predict the settling times of all manner of mixtures:
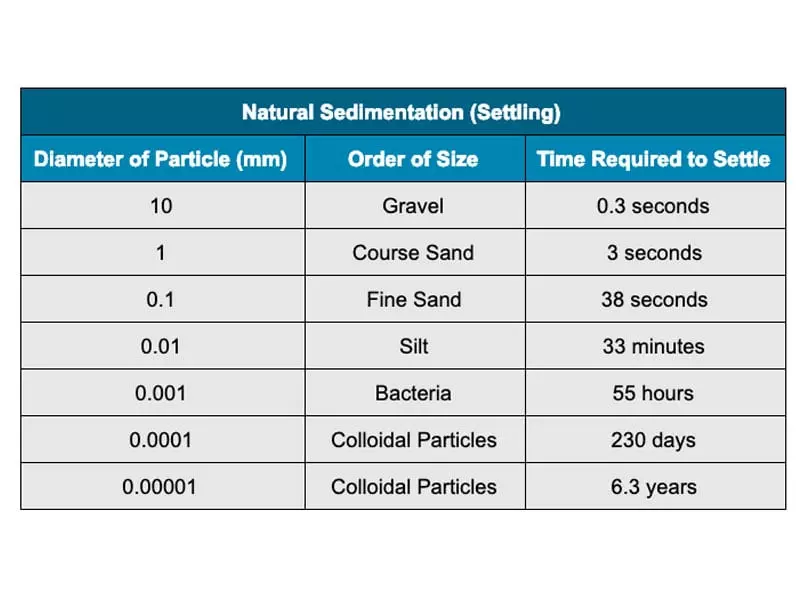
Here’s another way of stating Stokes’ Law—one that unlocks how we can take control of that settling process:
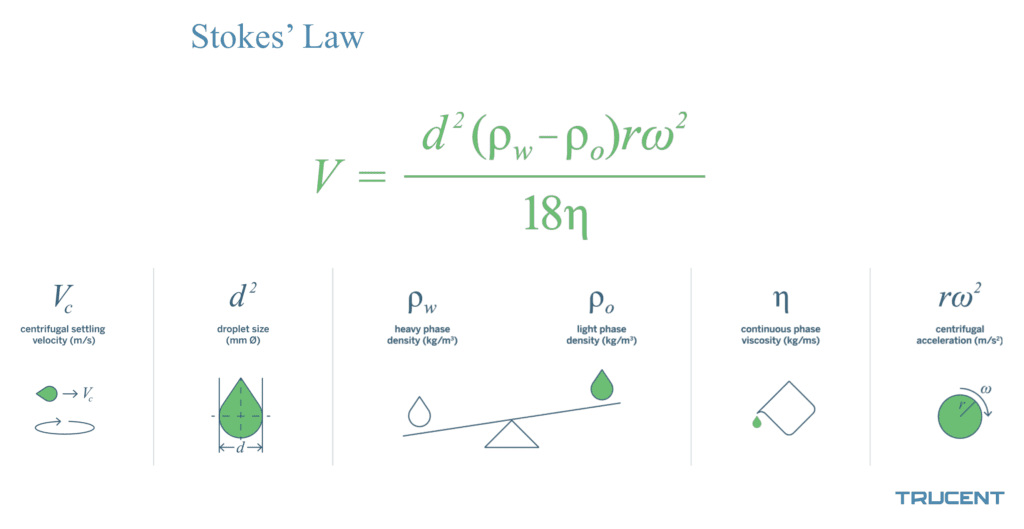
This tells us that the speed at which oil globs or particulate will separate from your fluid can be calculated by multiplying the droplet/particle size, the difference in the densities of the fluids, the speed the centrifuge is spinning (which is akin to the gravity working on that settling tank or bottle of Italian dressing), and dividing all of the by the viscosity of the oil/water mixture.
Do we want to speed up the separation? Stokes’ Law tells us we have four “levers” we can pull to control this process:
- droplet/particulate size: Bigger clumps/globs separate faster
- densities different: The bigger the difference in densities, the faster the separation
- fluid viscosity: Lower viscosity means faster separation
- force being applied: The greater the force, the faster the separation
Tweaking Stokes’ Law
By spinning a fluid in a centrifuge, we create additional artificial gravity—and thus control one factor in Stokes’ equation and massively speed the settling process. But this isn’t just about speeding up the settling process. A spinning centrifuge forces denser materials to its outer edge (causing the less dense materials to flow toward the center of the bowl). By carefully tuning the shape of the bowl, interior structure of the chamber, and speed at which it spins, we can separate fluids and solids with a surprising degree of accuracy and efficiency.
For example, in a single pass, your industrial centrifuge can either separate the solid particles out of a liquid (so-called “two-phase separation“) or separate several different fluids and remove solids (“three-phase separation“)—all in a single pass.
Centrifugation is just the beginning. Combining the right centrifuges, the right chemistry, and a thorough appreciation of Stokes’ Law is doubling yields and increasing efficiency every day.
